江苏教师招聘考试:数学专业简答题、教学设计题模拟题
2017江苏教师招聘考试培训
苏文江苏教师招聘考试交流qq群:179234145
苏文教育订阅号:NJSW_3103
简答题
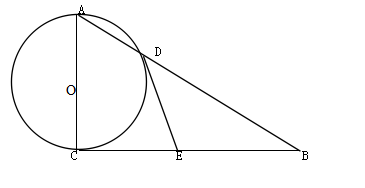
1、如图,在Rt△ABC=90,以AC为直径的园O与AB边交于点D,过点D作园O的切线,交于BC与点E。
(1).求证EB=EC
(2).若以点O.E.D.C.为顶点的四边形是正方形,是判断△ABC的形状,并说明理由。
2、

(1)求在未来连续3天里,有连续2天的日销量不低于100个且另一天的日销量低于50个的概率。
(2)用X表示在未来3天里日销量不低于100个的天数,求随机变量X的分布列数及期望E(X)及方差D(X)。
案例分析
下面是《勾股定理》一课的教学片段:
【新课引入】听故事,想问题:相传2500多年前,古希腊著名数学家毕哥拉斯去朋友家做客。宴席上,其他宾客在心情欢乐,毕哥拉斯却盯着朋友家的地面砖发呆。原来,地砖铺成了由许多个直角三角形组成的图案,黑白相间,非常美观。主人正纳闷时,毕哥拉斯突然恍然大悟,原来,他发现了图案中三个正方形的面积存在某种数量关心,从而通过此关系还发现了等腰三角形三边的某种数量关系。同学们,地砖图案中蕴含着怎样的数量关系呢,让我们一起探索吧。
【后续教学环节】接下来,在老师的引导下,在小组合作中,同学们发现了以等腰直角三角形两直角边为边长的小正方形的面积和,等于以斜边为边长的大正方形的面积,及等腰三角形三边之间有特殊关系:斜边的平方等于两直角边的平方和。再接下来,在网格中探索得到其他的直角三角形也有上述性质,由此猜想出勾股定理。
根据以上材料,请你回答下列问题:
1、从教学方法角度分析该科的新课引入的教学方法及合理性;
2、从教材把握的角度分析《勾股定理》该课在初中数学教学的地位和作用;
3、从三维课程目标的角度分析上述教学设计落实哪些教学目标?
答: 1、新课程标准指出数学教学活动应激发学生兴趣,调动学生积极性,引发学生思考,注重采用启发式教学方法,以上材料中采用了讲故事的方法引入新课,该教学方法表现出学生的认知发簪水平和已有的经验,能较好地激发学生学习兴趣,通过地砖图案中蕴含的数量关系的探索,体现古希腊注重启发式教学方法。
2、《勾股定理》这一课在初中数学地位与作用如下:
《勾股定理》是在学生已掌握了直角三角形有关性质的基础上进行学习的,在初中数学中起到承上启下的作用,为下面学习勾股定理的逆定理作好了铺垫,为以后学习“四边形”和“解直角三角形”奠定了基础。《勾股定理》的探索与正面蕴含这丰富的数学思想和科学研究方法,是培养学生良好思考品质的载体,它在数学的发展过程中起着重要作用,是数与形结合的典范。
3、从上述教学设计来看落实如下教学目标:
(1)知识与技能,经历观察,猜想,验证的探索过程、掌握了勾股定理
(2)数学思考:在勾股定理探索中,体会数形结合思想,发展合情推理能力
(3)解决问题:通过活动,体验数学思维严谨性,发展了形象思维
(4)情感态度,在探究活动中,培养学生的合作交流意识和探索精神
四、教学设计
内容:探索并证明“三角形内角和定理”
(学生基础:已经学习相交线,平行线的性质与判定。)
要求:1、只写出探索和证明两个环节的教学设计片段
2、要说明每个教学环节的设计意图
答: 1、探索《三角形内角和定力》教学片段
师:我们知道三角形有三个角,哪位同学告诉老师三个角的和是多少?
生:180°
师:你是怎么知道的?
生:猜的
生:可以把两个角写下来,与第三个角拼到一起,形成一个平角,就是180°
师:(课件语言)
生:还可以用量角把每一角量一遍,再加起来
师:太棒了,那大家动手量量看,加起来看看是不是180°
师:今天老师没带量角的,也不想问谁借,那你们能不能用已学过的知识证明出三角形内角和为180°呢?
生:不会
师:我们已经知道一个平角是180°,还学过平行线性质与判定,大家想象看能否用上,下面请同学们在小组内进行写作交流
设计意图:该教学环节,通过学生根据已有知识说出三角形内角和是180°,再引导学生通过动手操作,动手测量进行验证,培养了学生独立思考,自主探究的能力,进而引导学生利用已学过的知识进行转化,通过写作文交流进行探索证明,激发了学生的好奇心和求知欲,调动了学生的学习积极性,符合新课标提倡的学生是学习的主体,老师是学习的组织者、引导者和合作者。
2.证明《三角形内角和定理》教学片断
师:哪组派个表来证明一下你们组的成果
第一组
生:画图 生:写证明过程
连A点作直线EF//AB
∴
有∵
∴
师:这个小组是把三角形三个内角转化为一个平角的方法,利用了平行线的性质证明的?但是我们证明一个命题
三角形内角和是180,要先写出已知,在进行证明
请大家写出来吧(一人演板)师生一起规范写法
师:大家想想看还有其他证明方法吗?
第2组
生:画图 生:写证明过程
师:这个小组是把三角形三个角转化为了同等内角,再用平行线的性质证明的,可见的做平行线,利用平行线性质证明是较好的思路,下面在讲几种方法,供大家想想如何证明?
方法一:延长BC至D,作CE//AB

方法二:作BD//AE//CF
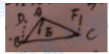
方法三:在BC上取一点D,作DE//AB,DF//AC
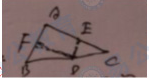
设计意图:在证明《三角形内角和定理》时,主要采用了启发式教学,引导学生利用转化的教学思想和已学过的知识进行证明,并组织学生进行合作特定小组汇报的形式进行教学,培养了学生创新思维能力和合作精神,符合新课程提倡的教学活动是师生积极参与,交往互动共同发展的过程。